1 三平方の定理に関心を持ち,直角三角形の性質を調べようとしたり,定理を活用 しようとする. 数学への関心・意欲・態度 2 直角三角形の3辺の長さの間の関係を見いだし,三平方の定理を用いて,図形の 性質を考える ことができる.3辺とも入力されている場合は、斜辺(c)が計算されます。 計算をやり直す場合は「クリア」ボタンを押すと入力された数値が削除されます。 目次 三平方の定理の解説; 3 小学生が導き出す 手助け問題 31 (1) 三角形abcの面積;
かみのドリル 三平方の定理
3平方の定理 面積
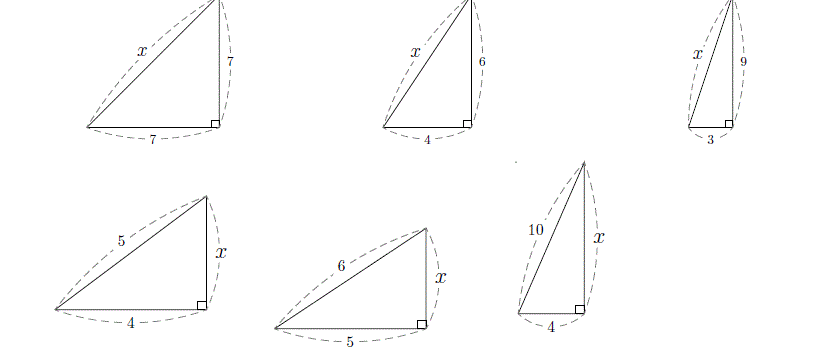
3平方の定理 面積- ここで,\(k=1\) であれば 2 平方定理が示されたことになります. \(k>1\) のとき, \(k/2b2=c2 が成り立ちます.これを「 三平方の定理 」といいます. 見かけ上「 斜めに見えている辺 」が斜辺なのではない 「 直角の向かい側 」にある辺=「 一番長い辺 」が斜辺 例1 直角をはさむ2辺の長さが与えられると斜辺の長さが求まります. 3222




三平方の定理の証明と使い方
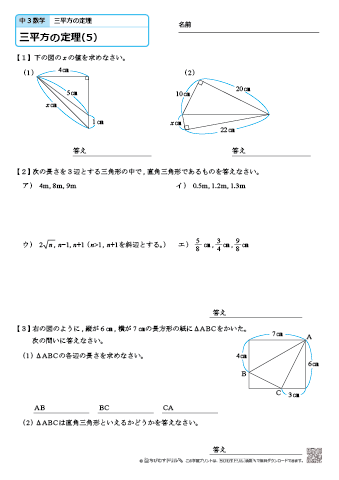
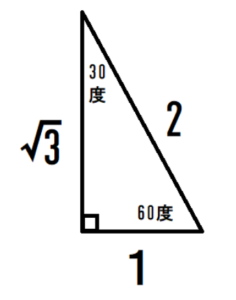
三平方の定理とは、別名「ピタゴラスの定理」とも呼ばれる、とても古くからある数学の定理です。 具体的にはCを直角とする直角三角形ABCの辺 a,b,c a, b, c について、 a2 b2 = c2 a 2 b 2 = c 2\(3\) 辺の比は暗記で、\(21\sqrt{3}\) です。 次に、右の直角三角形に三平方の定理を使うと、 最後の \(1\) 辺の長さが求まります。 最後の \(1\) 辺の長さを \(y\) とすると \(y^28^2=10^2\) \(y^264=100\) \(y^2=36\) \(y=±\sqrt{36}\) \(=±6\) この問題では、もちろん \(y\) は正の値なので三平方の定理の証明 AB=c, BC=a, AC=b, ∠ACB=90°の直角三角形ABCと合同な直角三角形を図のように並べて正方形ABDFをつくる。 正方形ABDFの面積をSとすると、1辺がcなので S=c2 ① また、正方形ABDFは△ABCと合同な三角形4つと正方形EGHCでできている。
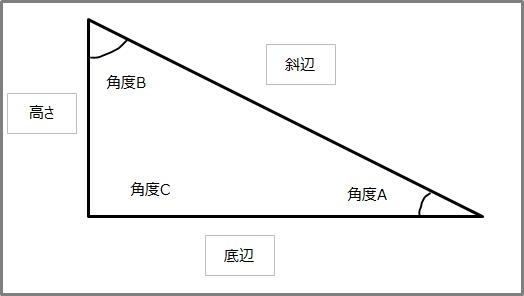
三平方の定理は、 直角三角形の三辺をa,b,cとする。 斜辺 (最も長い辺)をcとすると、 c² = a² b² が成り立つ というものです。 別名ピタゴラスの定理とも呼ばれます。 式は綺麗ですが、二乗が出てきます。 なので、実際にこの定理で辺の長さを計算すると、平方根を求める作業が必要になり、大変かもしれません。 三平方の定理とは,直角三角形において各辺の関係は 斜辺 2 = 底辺 2 + 高さ 2次のような直角三角形の3辺の長さについては, a 2 b 2 =c 2 が成り立ちます.(これを 三平方の定理 といいます.)
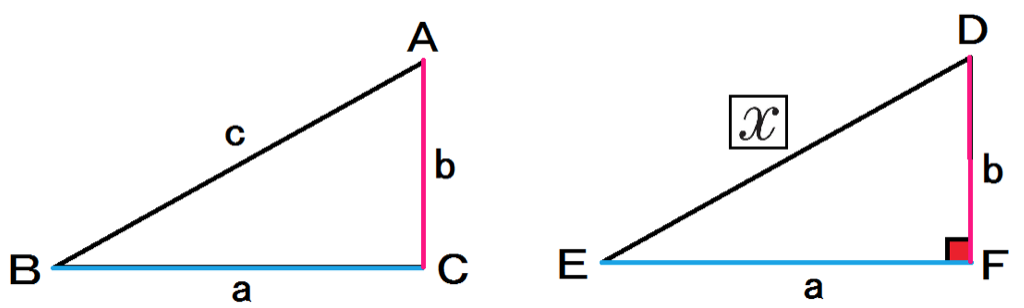
中学3年で学習するピタゴラスの定理(三平方の定理)は、その後の数学の学習で繰り 返し用いられる重要な定理である。 ピタゴラスの定理(三平方の定理) 左図のような直角三角形ABCにおいて、 a 2 +b 2 =c 2 が成り立つ。 逆に、上式が成り立つような3辺 a,b,c をもつ三 角形は直角三角形三平方の定理とは 直角三角形のときに利用できる 辺の長さの関係式でしたね。 それを発展させて考えていくと 直角三角形だけでなく 鋭角、鈍角三角形を見分ける方法として活用することができます。 入試などでは、活用する機会は少ないと思いますルジャンドルの3平方和定理は,どのような数が4つの正の平方数の和として表されるか否かを決定するというわけです. (証明)8k+3の形をした数は3つの奇数の平方の和として表せることは前述したとおりですが, 8k+3の形の数から4^2を引くと → 8k+3の形の数 となることからも,3つの平方



Studydoctor三平方の定理と四角形への利用 中学3年数学 Studydoctor



中学3年生 数学 三平方の定理 練習問題プリント ちびむすドリル 中学生
三平方の定理というと, 直角三角形において, (斜辺の2乗) = (他の2辺の2乗の和)4 中学受験に出る 直角三角形 41 三角定規動画一覧や問題のプリントアウトはこちらをご利用ください。ホームページ → http//19chtv/ Twitter→ https//twittercom/haichi_toaru




三平方の定理 自動計算サイト




中学数学 三平方の定理 特別な直角三角形 中学数学の無料オンライン学習サイトchu Su
つまり、下図のようになるよ! ということは、各頂点から点Pまでの長さが 6 6 だから、三平方の定理を用いると、 x2 = 62 –22 x 2 = 6 2 – 2 2 ∴ x2 = 36− 4 = 32 x 2 = 36 − 4 = 32 ∴ x = 4√2 x = 4 2 (x>0より) これを図にするとこう!直角三角形においては三平方の定理が成り立つため,3つの角が30°,60°,90°である直角三角形と,45°,45°,90°である直角三角形の3辺の長さには,それぞれ次のような関係が成り立っています。 となります。 となります。 が成り立ちます。 これを「三平方の定理」 といいます。三平方の定理 \(「a^2b^2=c^2」\) に \(a=3,b=5\) を代入すると \(3^25^2=c^2\) ⇔ \(925=c^2\) ⇔ \(34=c^2\) よって、\(c=\sqrt{34}\) となります。 \(\sqrt{34}\) は「\(34\) の正の平方 根」と言って、二乗したら \(34\) になる正の数のことを指します。 \(\sqrt{34}×\sqrt{34}=34\) Tooda Yuuto 具体的な値で表すと \(\sqrt{34}=51\cdots




中3数学 三平方の定理 で最も重要なポイントとは 映像授業のtry It トライイット




三平方の定理の利用 四角錐 円錐 チーム エン
四平方の定理とは 四平方の定理 とはひとことでいうと三平方の定理の3次元空間バージョンです. そう,四平方の定理はかの有名な三平方の定理さんと親戚のような関係なんです笑. 三平方の定理だと, $$ { a }^ { 2 } { b }^ { 2 }= { c }^ { 2 }$$ ですが四平方この定理の逆も成り立つ。すなわち、三角形の1辺の平方が他の2辺の平方の和に等しければ、始めの辺に対する頂角は直角である。この逆定理の成立によって、たとえば、辺の長さが3、4、5である三角形は3 2 +4 2 =5 2 であるから、直角三角形となる。この3三平方の定理に当てはめる。 x 2 1 2 =3 2 x 2 =91 x 2 =8 x=±2 2 x>0よりx=2 2 答 2 2 cm 確認次のそれぞれの三角形で、頂点Aから辺BCにおろした垂線の長さを求めよ。 答表示 1辺8cmの正三角形 A B C 4 3 cm AB=AC=29cm, BC=40cmの二等辺三角形 A B C 21cm 円と三平方 弦の長さ 円の中心から弦に垂線を引くと、弦の



1




Excel 三平方の定理で直角三角形の辺の長さ 面積 角度を求める わえなび ワード エクセル問題集
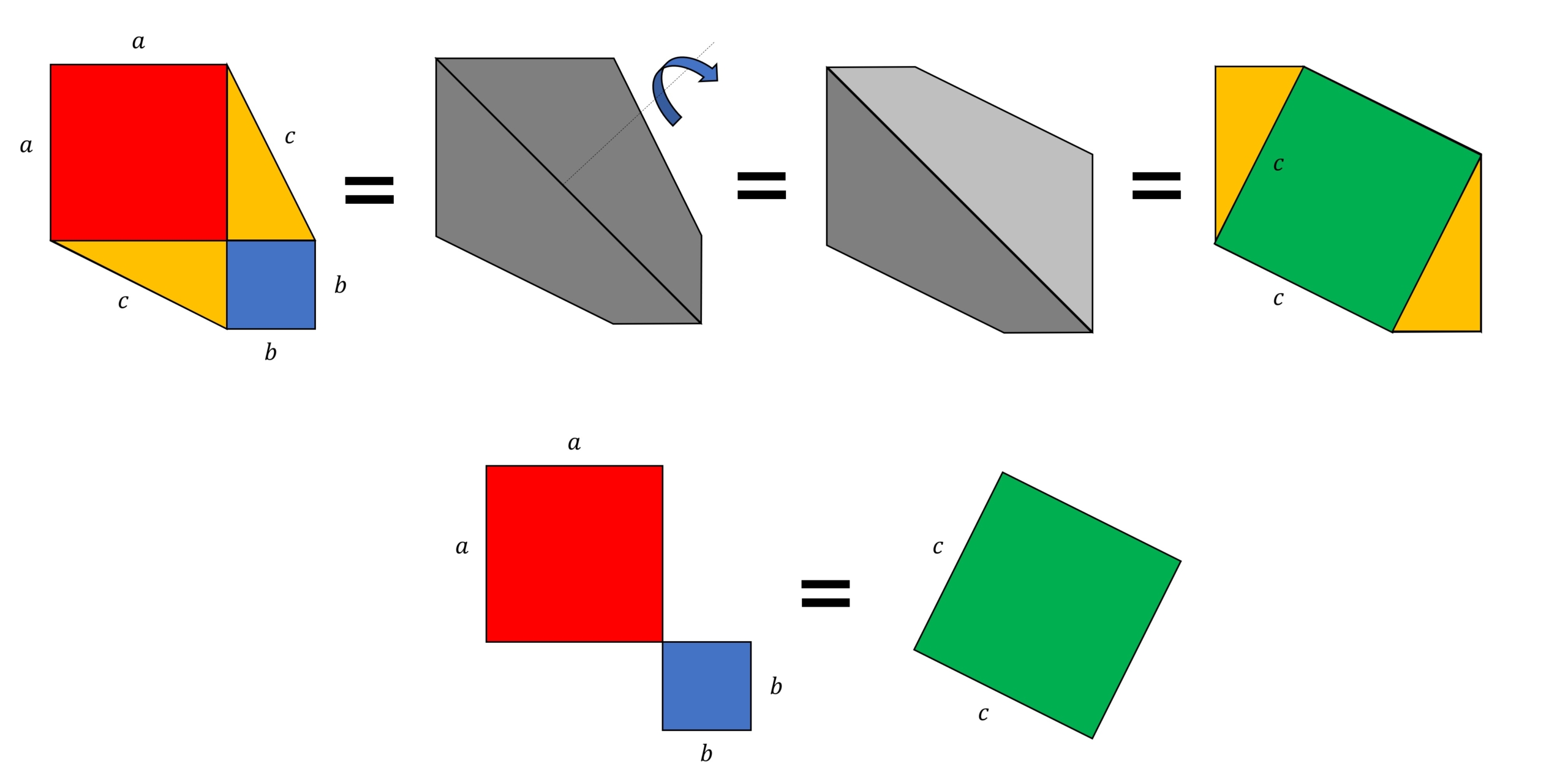
三平方の定理 直角三角形の三辺の長さを a、b、c とすると、 正方形P の 面積 c 2 は a+b を 1辺 とする正方形の面積から 4 つの合 同な直角三角形の面積を引いたものと等しいよね。 だから、 正方形P の面積は次のよう ピタゴラスの定理(3平方の定理)とは ピタゴラスの定理っていうのは、 直角三角形の3辺の長さの関係を表したものだよ その関係っていうのは、$斜辺^2=底辺^2高さ^2$だよ 辺の長さを求める時は、この式に当てはめることで求めることができるよ三平方の定理とは? 下図1のような直角三角形ABCの3つの辺abcには、次のような式が成り立ちます。 ① (斜辺の2乗は他の2辺の2乗の和に等しい) これを三平方の定理といいます。 三平方の定理の計算方法 図1の3つの辺abcを三平方の定理を使って求めてみましょう 1、辺cを求める




三平方の定理 ピタゴラスの定理




中学3年生 数学 三平方の定理 練習問題プリント ちびむすドリル 中学生
三平方の定理を使って直角三角形の辺の長さを求める4つの問題 三平方の定理をつかった問題でよく出てくるのは、 直角三角形の辺の長さを求める問題。 今日はこの問題を4つのパターンに分けてみたぞ。 超基本タイプ;直角三角形の3辺の長さに関する a 2 b 2 =c 2 という関係はピタゴラスの定理(三平方の定理)と呼ばれます。 この定理はその名の通り古くから知られていますが、本当にピタゴラス(cBC570cBC500)が発見したかどうか確証があるわけではありません。直角三角形AOPで三平方の定理を用いる。 A B O 2cm P x 6cm AO=6cm(半径), OP=2cm, AP=xcm x 2 2 2 = 6 2 x 2 = 32 x>0 より x=4 2 よってAB=8 2 ② 接点を通る半径と接線は垂直なので∠OAP=90° 直角三角形OAPで三平方の定理を用いる。 A P O 5cm 10cm x OA=5cm(半径), OP=10cm, AP=xcm x 2 5 2 =10 2 x 2 =75 x>0より x=5 3 次の問いに答えよ




ウケる数学 三平方の定理で解く 地平線までの距離 中日新聞web




三平方の定理の練習問題10問 解き方の解説 数学fun
4 k 3 4k3 4k 3 型の素数の指数が全て偶数 高々2つの整数の二乗和で表される整数はどんなものか? という疑問に答える非常に有名な定理です。 この定理を知っていることで数学オリンピックで有利になることはないと思いますが,整数論の様々な知識を



ベクトルの長さを三平方の定理を使って求める




高校数学 第2余弦定理 三平方の定理の一般化 と第1余弦定理の証明と利用 受験の月




Mathematics 三平方の定理 3 いろいろな三角形 働きアリ



Studydoctor三平方の定理と色々な三角形の面積 中学3年数学 Studydoctor




数学 三平方の定理 中学生 数学のノート Clear




三平方の定理の計算 この問題は絶対にできるようになろう 中学や高校の数学の計算問題




三平方の定理の証明と使い方
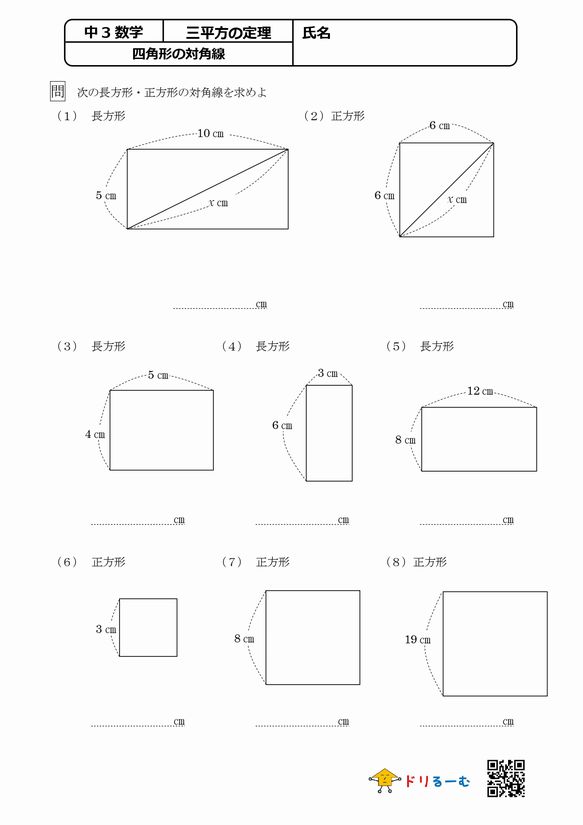



三平方の定理 四角形の対角線 ドリるーむ




カーナビはなぜ正確なの その秘密 三平方の定理 で教えます 横山 明日希 ブルーバックス 講談社 1 4



Studydoctor二等辺三角形や台形の面積と三平方の定理 中学3年数学 Studydoctor




中3数学 三平方の定理 で最も重要なポイントとは 映像授業のtry It トライイット




三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学




三平方の定理で ルートがつく計算になるのはなぜですか Clear




三平方の定理を英語で読んでみる




中学3年生 数学 三平方の定理 練習問題プリント ちびむすドリル 中学生
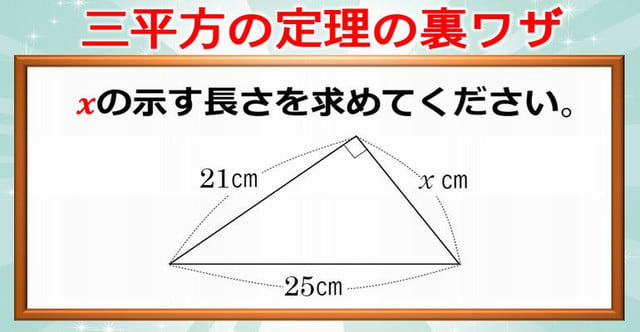



三平方の定理の裏ワザ 賢く解きたい計算の裏ワザ 暇つぶしに動画で脳トレ




中3数学 図でよくわかる三平方の定理 ピタゴラスの定理 の証明と計算問題 Irohabook




3分で理解 三平方の定理 ピタゴラスの定理 とその証明を完全解説 Rikeinvest




三平方の定理の応用




三平方の定理を簡単に理解 更に理解を深めよう 中学生 数学 公式 家庭教師のアルファ プロ講師による高品質指導




三平方の定理の証明 相似を利用した証明1 Fukusukeの数学めも




中3 数学 三平方の定理を完全攻略 中学生 数学のノート Clear




中3数学 三平方の定理 で最も重要なポイントとは 映像授業のtry It トライイット




数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo



三平方の定理の計算 角度と長さ Nujonoa Blog



三平方の定理とは 証明や計算問題 角度と辺の比の一覧 受験辞典




三平方の定理について考える4 三角形の相似を使った証明方法 身勝手な主張



三平方の定理 公式を簡単に覚える方法 中学数学 札幌市 学習塾 受験 チーム個別指導塾 大成会




三平方の定理 ピタゴラスの定理 と公式の証明 忍者が用いた三角の知恵 アタリマエ



感銘を受けた数学 三平方の定理の美しき証明たち 数学 統計教室の和から株式会社



三平方の定理 アメリカ合衆国大統領の証明 数々のたのしみ




三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ




三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ




円を利用した三平方の定理の証明 数学の面白いこと 役に立つことをまとめたサイト



中3数学 2分でわかる 三平方の定理の逆 Qikeru 学びを楽しくわかりやすく




三平方の定理の4通りの美しい証明 高校数学の美しい物語




三平方の定理 ピタゴラスの定理 とは 応用問題パターンまとめ10選 遊ぶ数学



三平方の定理が一瞬で理解できる 公式 証明から計算問題まで解説 Studyplus スタディプラス
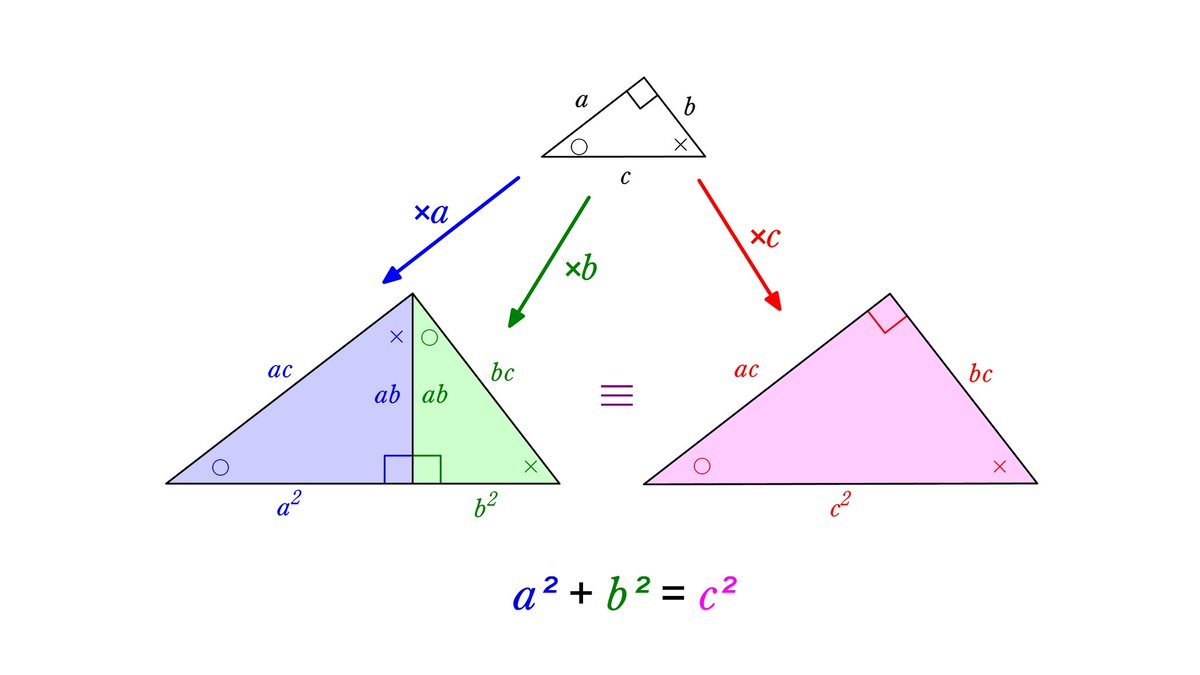



ポテト一郎 三平方の定理 一番好きな証明です




数学 中3 61 三平方の定理 基本編 Youtube




数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo



1



三平方の定理




三平方の定理 無料で使える中学学習プリント




三平方の定理 特別な直角三角形 イ弋マ本ゼミナール




3分でわかる 三平方の定理の公式と証明 利用と問題例 合格サプリ
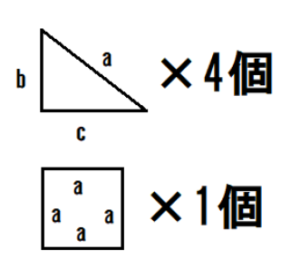



三平方の定理 公式を簡単に覚える方法 中学数学 札幌市 学習塾 受験 チーム個別指導塾 大成会
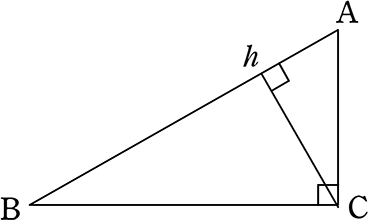



中学数学 三平方の定理




中学3年生 数学 三平方の定理 練習問題プリント ちびむすドリル 中学生




必見 絶対知りたい三平方の定理の証明方法3選 見やすい図で即わかる 高校生向け受験応援メディア 受験のミカタ




三平方の定理で辺を求める Youtube
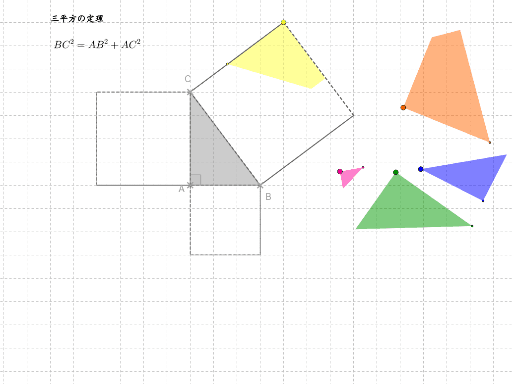



三平方の定理 Geogebra




三平方の定理 特別な直角三角形の3辺の比 中学生からの勉強質問 数学 進研ゼミ中学講座




三平方の定理の証明と使い方




國三 Junior High数学的 数学 三平方の定理 筆記 Clear
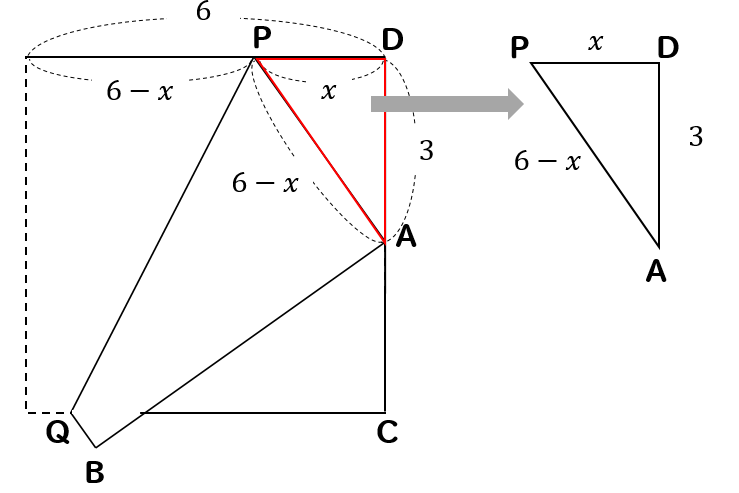



三平方の定理 方程式を利用する発展問題を解説 数スタ




三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ




感銘を受けた数学 三平方の定理の美しき証明たち 数学 統計教室の和から株式会社
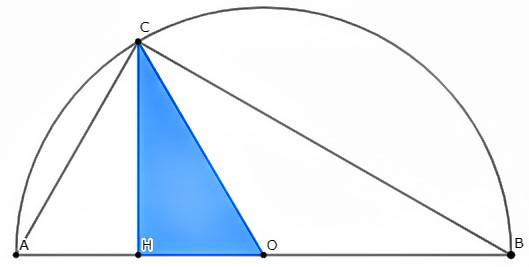



File 三平方の定理 Jpg Wikimedia Commons




三平方の定理 ピタゴラスの定理 の計算問題 の3つの解き方 Qikeru 学びを楽しくわかりやすく



三平方の定理の導入 Geogebra




数学 三平方の定理 証明 図形的に オンライン無料塾 ターンナップ Youtube




三平方の定理 覚えること 三角定規 苦手な数学を簡単に
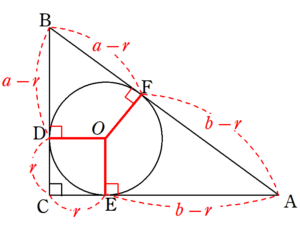



三平方の定理の証明 内接円の利用 Fukusukeの数学めも



三平方の定理




三平方の定理 ピタゴラスの定理 の公式と計算方法 リョースケ大学




中3数学 三平方の定理の応用 75度に要注意 Youtube




数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




かみのドリル 三平方の定理




三平方の定理を使って面積を求める方法は 問題を使って解説するよ 中学数学 理科の学習まとめサイト




高校数学 三平方の定理による三角関数の計算 1 映像授業のtry It トライイット
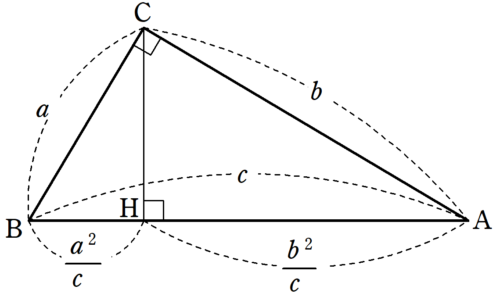



三平方の定理の証明 相似を利用した証明1 Fukusukeの数学めも




三平方の定理をパズルで証明 色んなパズルに挑戦してみよう 数学の面白いこと 役に立つことをまとめたサイト
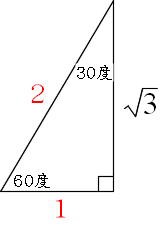



Mathematics 三平方の定理 2 特別な直角三角形 働きアリ




三平方の定理 ピタゴラスの定理 の計算問題 の3つの解き方 Qikeru 学びを楽しくわかりやすく



三平方の定理



三平方の定理




tan8とcos8であらわした三平方の定理の覚え方 Schoolmath S Diary
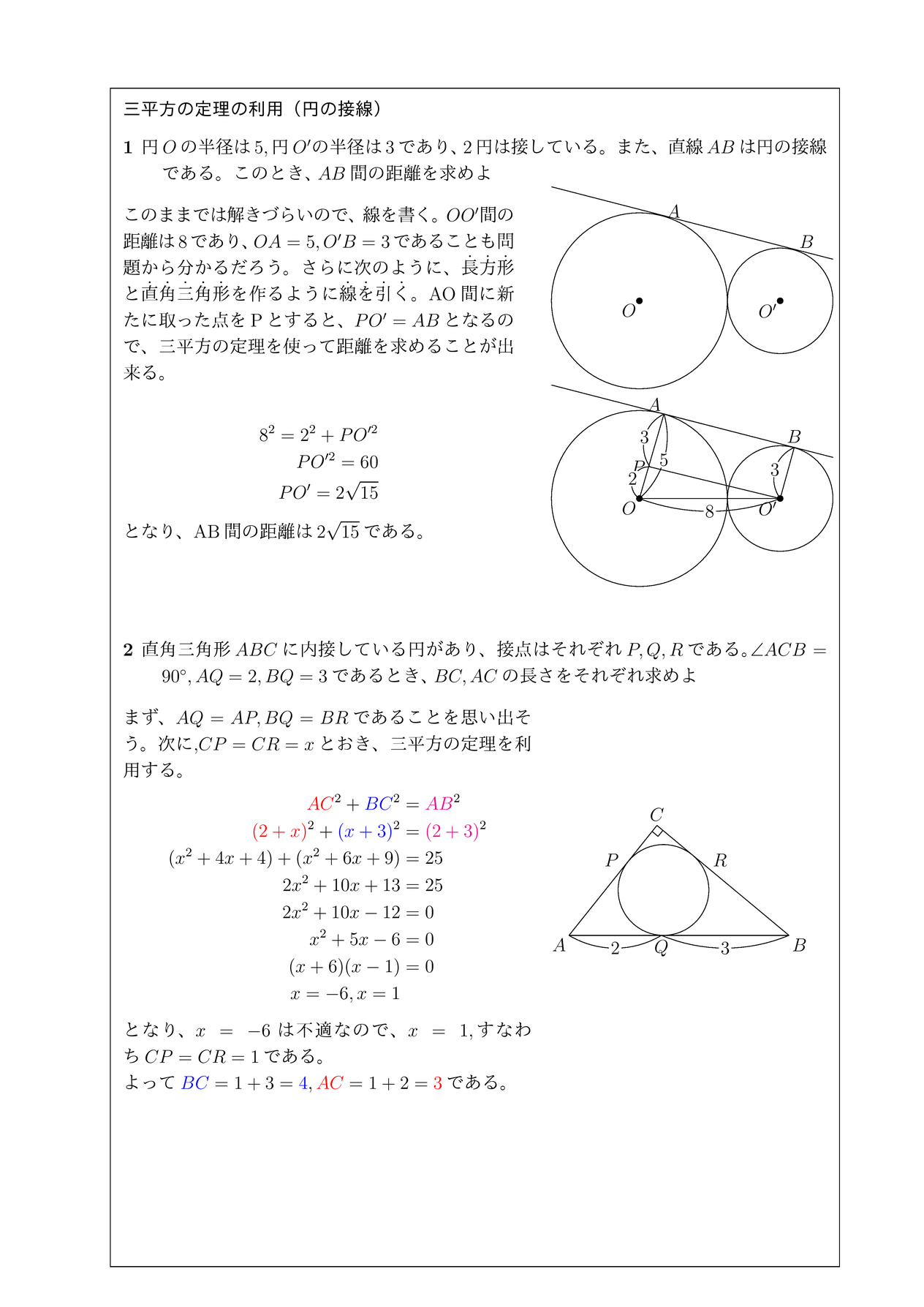



三平方の定理の利用 円の接線 チーム エン



三平方の定理が一瞬で理解できる 公式 証明から計算問題まで解説 Studyplus スタディプラス




三平方の定理 特別な直角三角形の比を使った計算のやり方は Youtube




三平方の定理の4通りの美しい証明 高校数学の美しい物語




三平方の定理 おやじさん ネット
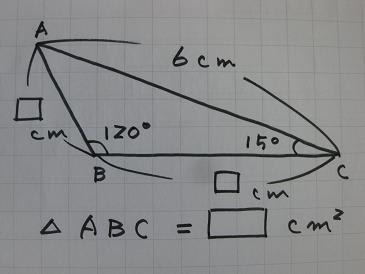



マッキーの教室 中2生徒の 三平方の定理 問題の質問に答える マッキーのつれづれ日記



Studydoctor特別な三角形と三平方の定理 中学3年数学 Studydoctor




三平方の定理 ピタゴラスの定理 と三角比の導入 教遊者




3分でわかる 三平方の定理 ピタゴラスの定理 の公式とは Qikeru 学びを楽しくわかりやすく




三平方の定理 ピタゴラスの定理 の証明まとめ5選 全部でいくつあるの 遊ぶ数学



Q Tbn And9gcq7h6dlzvq5e0plulfvxu64dpvadasyky0sizoi2drjv Uyz1m5 Usqp Cau



1




中学3年数学練習問題 三平方の定理の超基本




数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo



0 件のコメント:
コメントを投稿