立体の表面積 円錐 590060-立体の表面積 円錐

立体の表面積2 名前 1．右の図のような底面の円の半径が cm、母線の長さが cmの 円錐があります。 次の問いに答えなさい。 ①側面を展開した扇形の弧の長さを求めなさい。 ②側面を展開した扇形の中心角を求めなさい。 ③この円錐の表面積を求めなさい。円錐の表面積を求める公式 前述の通り、円錐の表面積 S を求める公式は、次の通りです。 S = πr(r R) = π ×（底面の半径）× {（底面の半径） （母線の長さ）} S = π r ( r R) = π × （底面の半径） × { （底面の半径） （母線の長さ） } この式に出てくる文字の意味は、次の通りです。 S 円錐の表面積（ S urface area） π 円周率（= 314）いろいろな立体の問題 第1節 体積における置換積分を身につけよう(その4) 体積の問題でも円錐を切った体積となると少し

空間図形 角柱 角錐 すい 円柱 円錐の体積の求め方 中学数学 定期テスト対策サイト

立体の表面積 円錐

立体の表面積 円錐-29/3/21 四角錐・三角錐の表面積 = 底面積 側面積 円錐の表面積 = 半径 × π ×(半径 母線)19/4/15 円錐の体積の求め方の公式は、底面積×高さ×1/3だったよね。 もう少し詳しくかいてあげると、半径×半径×円周率×円錐の高さ×1/3になるんだ。 これなら3秒で円錐の体積を計算できちゃいそうだね。 ただ、そのスピード感について来れないときもあるだろうから、今日は、円錐の体積の求め方をチョーゆっくり公式をつかってといてみるよ^^「円錐の体積の

中1 回転体の表面積と体積についてです 右の画像が模範解答です Clear

ベスト50数学 円錐 の 体積 の 求め 方 rita renata 年6月25日木曜日 Math 横にした円錐が転がる問題 中学生 働きアリ 計算公式 円錐の体積の求め方がわかる3つのステップ Qikeru 学びを 円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生3 角錐の表面積正四角錐 以下の立体の表面積を求めよう。 ① ② 4 円錐の表面積 以下の立体の表面積を求めよう。 ① 底面の半径が4cm、母線の長さが 12cmの円錐 ②B 2 x 2 = b 2 ( b h a − b) 2 = b a − b ( a − b) 2 h 2 よって、小さな円錐の側面積は、 円錐の側面積の求め方 を使うと、 π × b × b a − b ( a − b) 2 h 2 = π b 2 a − b ( a − b) 2 h 2 同様に、大きな円錐の側面積は、 π × a × a 2 ( x h) 2 = π a × a 2 ( a h a − b) 2 = π a 2 a − b ( a − b) 2 h 2 と

面積が円錐の表面積から底面の面積を引けば出るので 60π25π =35πcm2 弧の長さは底面の周と等しいので 10πcm 10π 35π x おうぎ形の面積 = おうぎ形の半径×弧÷2より おうぎ形の半径をxとすると 35π = x × 10π ÷2 x = 7 側面のおうぎ形の半径は母線の長さに直方体の表面積 V = 2(ab ah bh) V = 2 (a b a h b h) 表面積 = 2 × (たて × 横 ＋ たて × 高さ よこ × 高さ)27/5/ 円錐 円錐（えんすい，英 cone）とは，円を底面として持つ錐（きり）状にとがった立体のことである‥． Wikipedia先生によると円錐とはこのような立体のことらしいです． 今日は円錐についてのブログです． 表面積を求める公式 S = r π (r m) S = r π (r m)

公式計算 平面図形の面積（a），周長（l）および重心位置（g） p11 平面図形の性質 p12 立体の体積（v），表面積（s）または側面積（f）および重心位置（g） p12_1_幾何I_本冊2章smd Page 15 17 v340 8 空間図形の計量① 39 柱体の体積・表面積 ① 立体のすべての面の面積の和を表面積という。また，側面全体の面積を側面積，1つの底面 の面積を底面積という。 ② (柱体の体積)=(底面積)×(高さ)，(柱体の表面積)=(側面積)(底面積)×214/1/ この記事の目的：錐形を求める際に「3分の1」する理由を中学生にも分かるように説明する． はじめに 錐形は3分の1 指針 ①特別な四角錐を考える ②特別な三角錐を考える ③錐体の体積の求め方の根本を考える ④体積が変わると？ 最後に

立体の表面積の求め方 直方体 円錐 円錐台 バカでもわかる 中学数学

計算公式 円錐の体積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく

立体の表面積展開図（入試問題） → 携帯版は別頁 == 立体の表面積展開図（入試問題） == 要点11 ≪円柱の側面積≫ 円柱の表面積は，2つの底面積と側面積の和になります． 右図のように底面の半径が r ，高さが h である円柱の側面は長方形で，側面積は 2πr×h になります． ※以下に引用している入試問題で，元の問題は記述式ですが，この教材ではWeb上で(6) 円錐 次の球の体積と表面積を求めなさい。 (1) 半径6cmの球 (2) 半径3cmの半球 体積 体積 表面積 表面積 8cm 6cm 10cm 12cm 9cm 6cm 12cm 16cm 2cm 3cm 2cm 9cm 4cm 4cm 4cm 7cm 8cm 5cm 6cm 15cm 5cm 3cm 3cm 2cm 4cm 10cm 6cm 4cm 12cm 8cm 弧の長さ 2,*6* 60 360 =2,(cm) 面積 2 ,*6* 60 360 =6,(cm2)次の柱の表面積を求めよ。 底面が長方形の四角柱 5cm 10cm 6cm 円柱 4cm 9cm 底面が直角三角形の三角柱 12cm 13cm 15cm 5cm 次の錐の表面積を求めよ。 円錐 3cm 10cm 正四角錐 8cm cm

表面積の求め方 計算公式一覧

立体の表面積

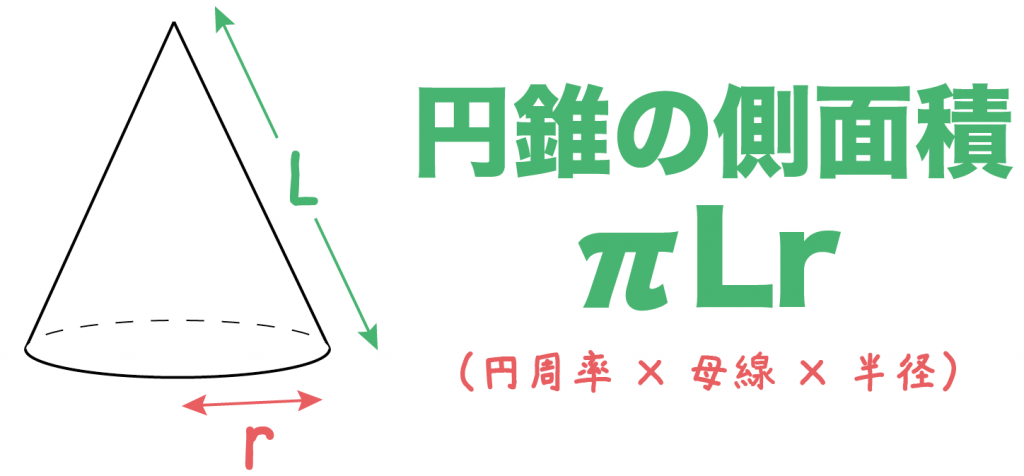
4/4/19 教科書 新編 新しい数学1 東京書籍, 単元 立体の体積と表面積, 「学校では教えてくれない、円錐の表面積の㊙️テクニックについて紹介します！ これができれば周りよりも速く問題を解くことができ、ライバルと差をつけられること間違いなし！！！」, 学年 中学1年生, キーワード 数学18/4/15 円錐の側面積の求め方 にはチョー簡単な計算公式があるんだ。 「円錐の半径」をr、「母線の長さ」をLとすると、 「円錐の側面積」は次の式で求めることができる。 πLr つまり、 （円周率）×（母線の長さ）×（底面の半径） ってことだね。== 立体の表面積(円柱，角柱，円錐，角錐の表面積) == 解説 立体の表面積は 「展開図」で考える とよく分かります。

円錐の表面積の求め方 公式と計算例

計算公式 円錐の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく

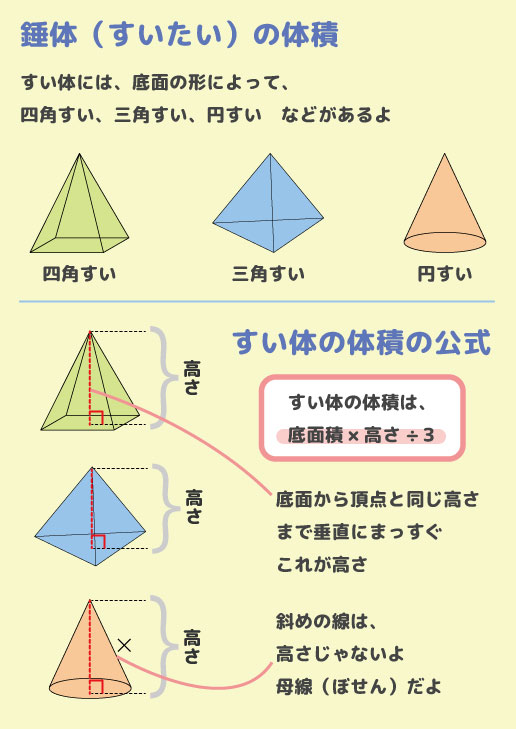
今回は 「立体の表面積」 を求めるよ。 「表面積」 って分かるかな。漢字のとおり、立体の 「表面の面積」 のことだよ。底面や側面など、 すべての面の面積 を求めて、たし合わせよう。立体の表面積 マウスで図を動かしたり拡大縮小ができます。 図をタッチ操作すると，動かしたり拡大縮小ができます。 図形を自分で操作できるCGアニメーションが表示されます。 スタートを押すとアニメーションが開始されます。ℎ 𝑉 = 𝑆ℎ 角錐や円錐の体積 𝑆 𝑆 底面積 ℎ 高さ 角錐や円錐の体積を𝑉，底面積を𝑆，高さをℎとして， 次の式から求められる。

下の図は半球と円錐を組み合わせた立体である この立体の表面積を求めなさい た Yahoo 知恵袋

球の表面積と体積の公式 数学fun

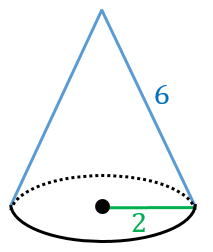
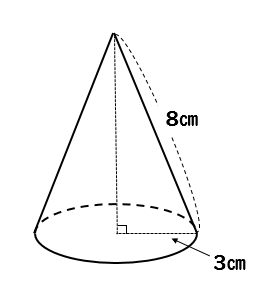
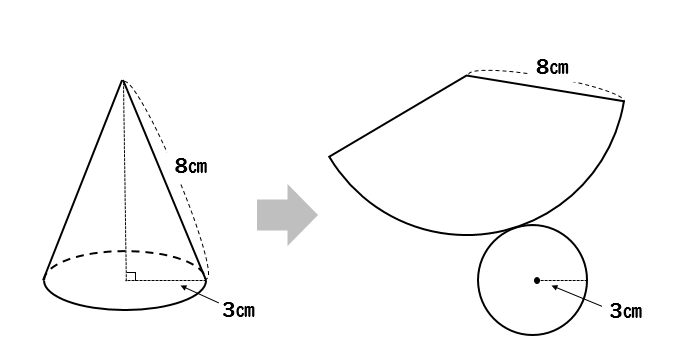
円錐の表面積、中心角を求める問題を丁寧に解説！ それぞれの問題を解説していきます。 下の図の立体についてそれぞれ求めなさい。 （1）この円錐を展開したときにできる側面のおうぎ形の中心角を求めなさい。 （2）この円錐の表面積を求めなさい。 その中でも円錐を取り上げた問題が一番よく出題されます。 空間図形の知識だけでなく、おうぎ形の知識もHello School 算数 体積・表面積 インターネット上で受験算数の一通りの基本的解法をマスターしよう♪。立体の体積の求め方 これで，円錐の体積が円柱の体積の 三分の一 になっていることが示されたのですが，以上の議論は，「任意の立体について，基準となる軸に対して軸と垂直な平面による切断面の面積が分かれば，その立体の体積を定積分により求めることができる。

1

立体の表面積の求め方 直方体 円錐 円錐台 バカでもわかる 中学数学

動画一覧や問題のプリントアウトはこちらをご利用ください。ホームページ → http//19chtv/ Twitter→ https//twittercom/haichi_toaru単元「空間図形」の小単元「立体の体積」（2時間）における数学的活動を取り入れた授業モデルです。 単元 空間図形 （啓林館） 2 立体の表面積と体積15/2/19 表面積とは、立体の表面の面積のことです。 公式を覚えてさえいれば簡単ですが、その公式が覚えられないという方も多いでしょう。 この記事では、そんな表面積についてまとめます。 ※以下の目次の項目を押すと、直接、説明に飛ぶことができます。

角錐 円錐の体積と表面積の公式 数学fun

円柱と円錐の違い 表面積や体積 展開図など調べてみたよ ヒデオの情報管理部屋

：n ならば 面積比は､m2：n2 である。 ② 相似な立体の表面積比は、相似比の2乗に等しい。 相似比がm： よって、円錐の表面積は、 ①② =9π15π = 24π・・・（答） となります。 円錐の表面積の公式を使って求めた場合 底面積側面積で円錐の表面積を求めるのに、加えて、円錐の表面積の公式を使った場合もみてみましょう。 円錐の表面積の公式は、 πr（mr）でした。30/3/11 1／3時 ・角柱や円柱の表面積を求めることができる。 ・角柱や円柱の表面積の求め方を理解する。 本時の学習内容「角柱や円柱の表面積の求め方を考えよう」を知る。 教科書143ページの「考えてみよう」に取り組む。 立体の「表面積」、「底面積

立体の表面積 無料で使える中学学習プリント

円錐台の体積と表面積を計算する公式と証明 具体例で学ぶ数学

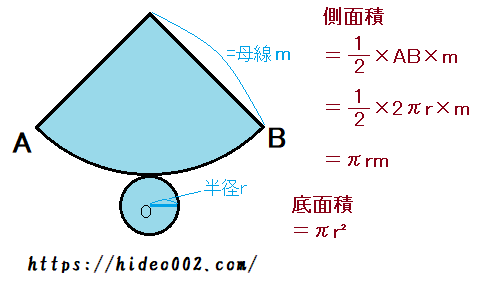
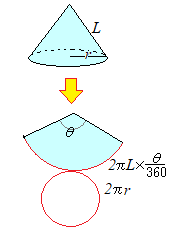
① （錐体の表面積）＝（側面積）＋（底面積） ② 円錐の底面の周の長さ（側面の扇形の弧の長さ）を ¬，母線の長さを R，側面積をS とすると， S＝ 1 2 ¬R ③ 円錐の底面の半径を r とすると，②より，S＝ 1 2 ×2∏r×R，すなわち，S＝∏rR ④ 側面の扇形の中心角は， r R ×360° 問題2 右の図の円錐の表面積を求めよ。29/9/16 立体の表面積を求める問題です。 考え方のポイント 立体の表面積は展開図を書いて考えましょう。 例）立方体は正方形が6枚 正方形の面積×6 ＊展開図が頭に思い浮かぶ場合は直接求めて構いませんが、よく分からない場合は自分で展開図を書いて長さを書いていくようにしてください。立体すべての面の面積を表面積という。 円柱の表面積 まずは展開図にしてみよう。 側面積 底面積 2 ＝9π 表面積 答え 78π c㎡ 円錐の表面積

円錐の表面積 Youtube

円錐の表面積の求め方 公式と計算例

8/9/19 ・ 立体の表面積の考え方 ①展開図を考える ②底面積、側面積をそれぞれ求める ③底面積と側面積を足し合わせる ・ 角柱の表面積 表面積=底面積\(\times2\)側面積 ・ 円錐の表面積 表面積=底面積(円)側面積(おうぎ形) 今回はここまでです。また，立体の表面全体の面積を表面積という。 角柱や円柱の表面積 ・・・(表面積) = (底面積) × 2 (側面積) 角錐や円錐の表面積・・・(表面積)= (底面積) (側面積) 球の表面積 𝑺・・・𝑆=4π𝑟2 （ 球の半径：r ） 1右の図の円錐について，次の問いに

公式を図解 すい体の体積 円すいの表面積の求め方

簡単公式 円錐の側面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく

円錐の側面積 底面積 表面積の求め方 具体例で学ぶ数学

公式一覧 立体の体積 表面積の求め方 円柱 三角柱 円錐 三角錐 球

円錐の表面積 中心角を求める問題を丁寧に解説 数スタ

角錐 円錐の体積と表面積の公式 数学fun

計算公式 円錐の体積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく

円錐の表面積の求め方 公式と計算例

至急です の求め方が分からないです 詳しく教えてくれる Clear

中1数学 円柱 円すいの表面積の求め方がサクッとわかる 映像授業のtry It トライイット

立体の表面積の求め方 直方体 円錐 円錐台 バカでもわかる 中学数学

立体の表面積

公式を図解 すい体の体積 円すいの表面積の求め方

円すいの展開図 表面積の求め方 公式があるの知っていますか

回転体の体積と表面積 中学数学の計算の求め方 リョースケ大学

円錐の表面積 Youtube

円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ

中学数学 回転体の体積 表面積を求める問題を解説するぞ 中学数学 理科の学習まとめサイト

19年前期 千葉県公立高校入試 数学 第5問 文章題 解答 解説 船橋市議会議員 朝倉幹晴公式サイト

誰でもわかる数学 中学１年 立体の表面積 円錐 Youtube

立体の表面積 無料で使える中学学習プリント

中１数学 すい体の体積と円すいの表面積 数学検定５級 お家でお勉強

中1数学 円柱 円すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット

円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ

円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ

円すいの展開図 表面積の求め方 公式があるの知っていますか

1

角錐 円錐の体積と表面積の公式 数学fun

立体 の 表面積 求め 方

中学数学 回転体の体積 表面積を求める問題を解説するぞ 中学数学 理科の学習まとめサイト

円錐の表面積 中心角を求める問題を丁寧に解説 数スタ

円錐の体積と表面積の求め方 押さえておくべき公式と解法の手順

円錐とは 体積 表面積の公式や求め方 受験辞典

中学数学 円錐の裏技集 暗算で中心角 側面積 表面積 中１数学 Youtube

円錐の表面積 中心角を求める問題を丁寧に解説 数スタ

計算公式 円錐の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく

この問図形の表面積と体積を教えてください 上の円錐と円柱 Yahoo 知恵袋

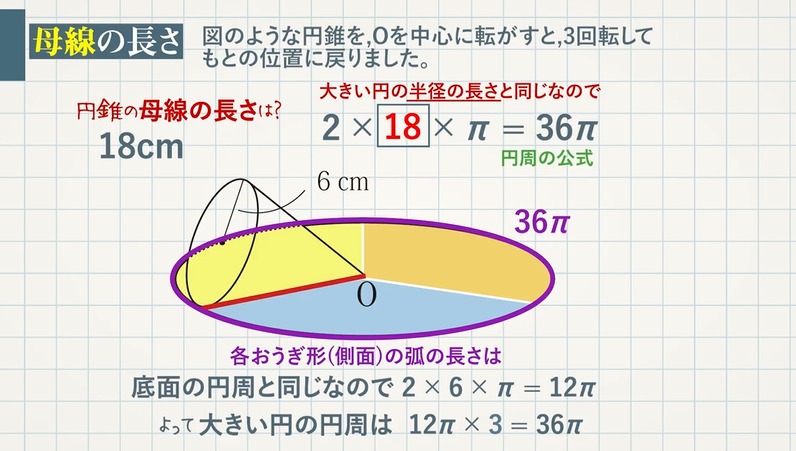
円錐 完全攻略 体積 弧の長さ 中心角 側面積 表面積 母線の長さ 教遊者

円錐とは 体積 表面積の公式や求め方 受験辞典

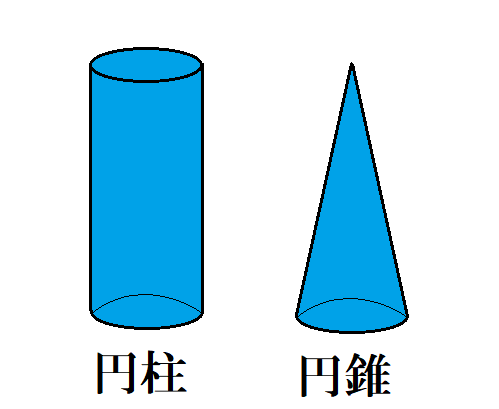
円柱と円錐の違い 表面積や体積 展開図など調べてみたよ ヒデオの情報管理部屋

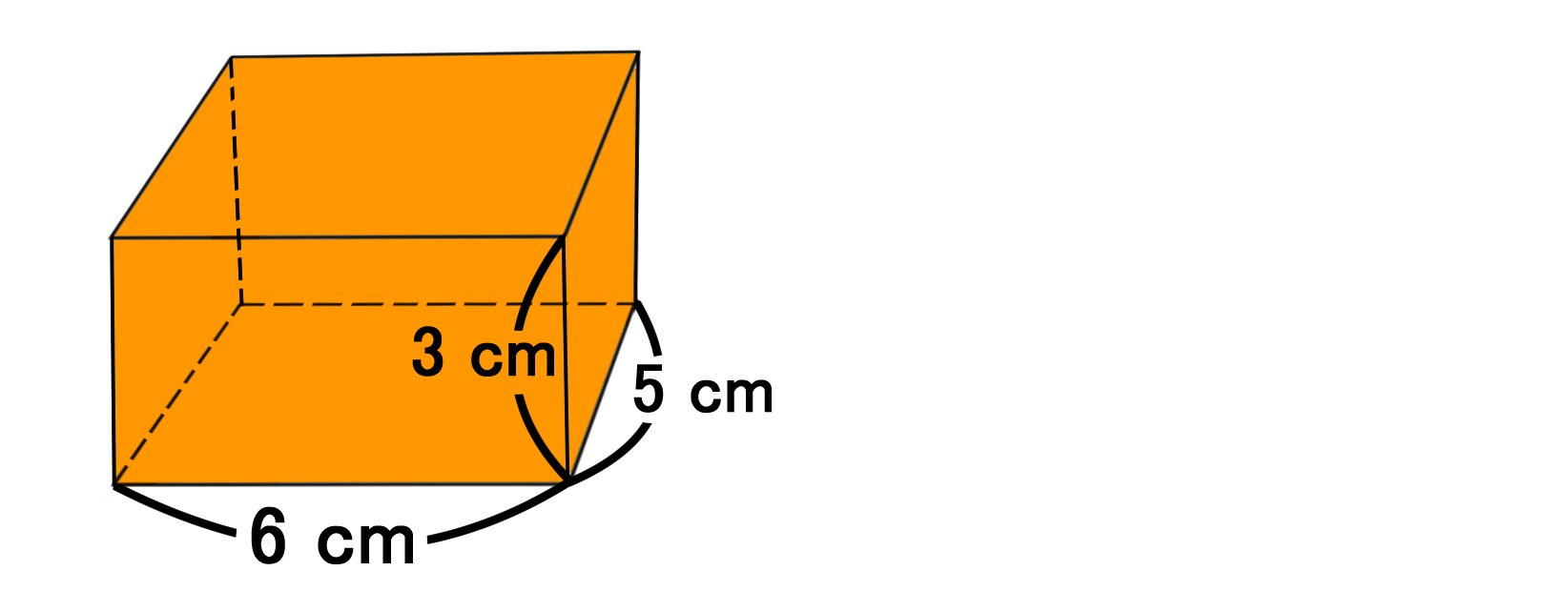
立体の表面積の求め方 直方体 円錐 円錐台 バカでもわかる 中学数学

角柱 円柱の表面積と体積の公式 数学fun

角錐 円錐の体積と表面積の公式 数学fun

計算公式 円錐の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく

中1 回転体の表面積と体積についてです 右の画像が模範解答です Clear

円錐の体積ってなんであの公式なの Webty Staff Blog

中3 三角形の相似 円錐の体積比 日本語版 Youtube

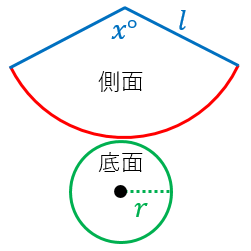
円錐の側面積 底面積 表面積の求め方 具体例で学ぶ数学

次の図は 大きな円錐から小さな円錐を切り取ったものです 次の問いに答えなさい Yahoo 知恵袋

6 17 第6章 空間図形立体の表面積と体積 円錐の表面積 ニュージーランド短期留学ダイアリー

Left 1right 5cm 1ocm Descubre Como Resolverlo En Qanda

円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ

下の図の円すいと円柱を合わせた立体の体積を求めなさい なお 円周率はpを用いる Yahoo 知恵袋

公式を図解 すい体の体積 円すいの表面積の求め方

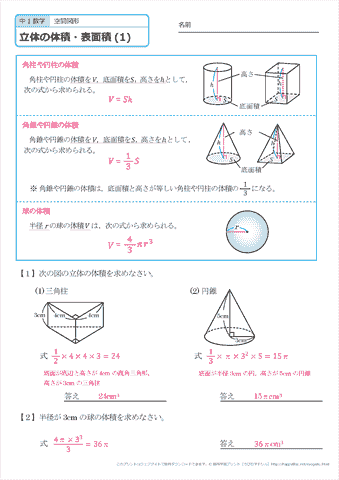
中学１年生 数学 空間図形 立体の体積と表面積 練習プリント 無料ダウンロード 印刷 ちびむすドリル 中学生

角錐 円錐の体積と表面積の求め方 錐体の公式と母線の概念 リョースケ大学

円錐 完全攻略 体積 弧の長さ 中心角 側面積 表面積 母線の長さ 教遊者

円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ

円錐 体積の比較 中学から数学だいすき

公式を図解 すい体の体積 円すいの表面積の求め方

3分でわかる 円錐の体積 表面積の求め方 合格サプリ

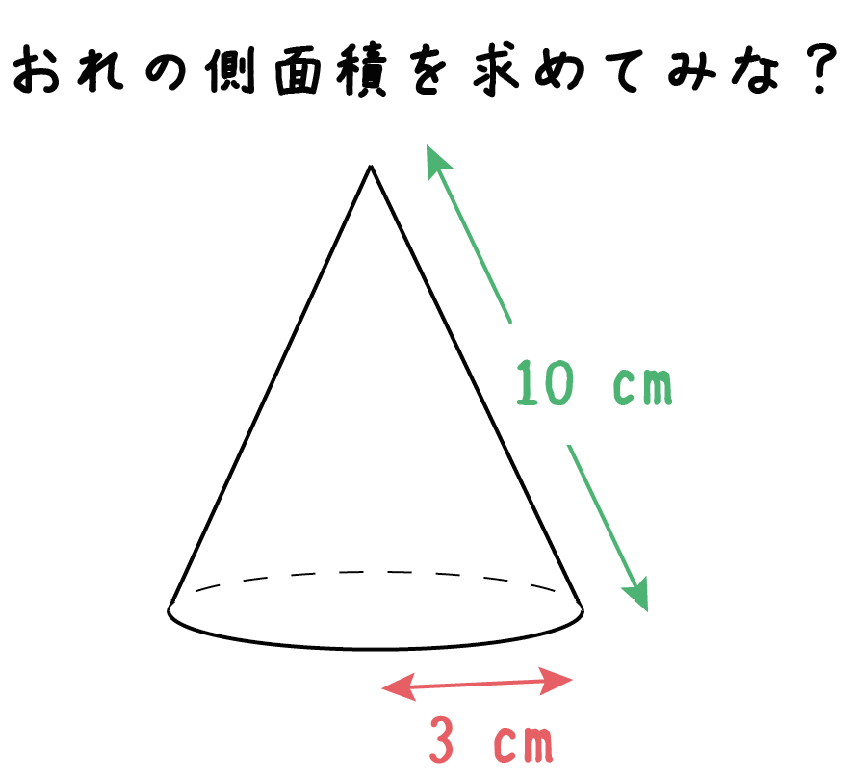
簡単公式 円錐の側面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく

中学数学 円すいの表面積 中学数学の無料オンライン学習サイトchu Su

中1数学 円柱 円すいの表面積の求め方がサクッとわかる 映像授業のtry It トライイット

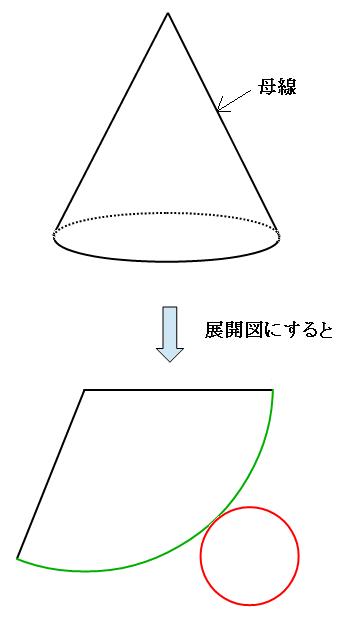
円錐の表面積の求め方を解説 円錐の表面積の求め方は完全パターン化できる

中1数学 円柱 円すいの表面積の求め方がサクッとわかる 映像授業のtry It トライイット

3d100 Descubre Como Resolverlo En Qanda

かみのドリル 立体の体積と表面積 回転

計算公式 円錐の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく

毎日問題を解こう 26 苦手な数学を簡単に

円錐の表面積の求め方 裏技の公式を覚えたらめちゃくちゃ簡単 中学や高校の数学の計算問題

円錐 完全攻略 体積 弧の長さ 中心角 側面積 表面積 母線の長さ 教遊者

Hd限定円錐 体積 の 求め 方 ページを着色するだけ

円錐とは 体積 表面積の公式や求め方 受験辞典

円錐の表面積の求め方を解説 円錐の表面積の求め方は完全パターン化できる

１つずつ丁寧に計算すれば解ける 円柱 の体積 表面積の求め方 お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード

1

角錐 円錐の体積と表面積の求め方 錐体の公式と母線の概念 リョースケ大学

働きアリ 数学科

円錐 完全攻略 体積 弧の長さ 中心角 側面積 表面積 母線の長さ 教遊者

空間図形14 円すい台の体積 Youtube

球の半分と円錐を組み合わせた立体です 体積と表面積を求めよ 教え Yahoo 知恵袋

円錐の表面積 中心角を求める問題を丁寧に解説 数スタ

空間図形 角柱 角錐 すい 円柱 円錐の体積の求め方 中学数学 定期テスト対策サイト

この体積の求め方を教えてください Clear

19年前期 千葉県公立高校入試 数学 第5問 文章題 解答 解説 船橋市議会議員 朝倉幹晴公式サイト

1

表面積と体積の比の問題 立体の相似比を出すのが一番最初だ 中学や高校の数学の計算問題

Incoming Term: 立体の表面積 円錐,